1. 가장 빠르게 가는 방법은 무엇일까요?
컴퓨터는 인간처럼 가장 빠르고 좋은 길을 찾기 위해 여러가지를 관찰합니다. 이를 탐색(Exploration)이라고 합니다. 컴퓨터에는 아주 방대한 양의 데이터가 있습니다. 이를 빠르게 찾기 위해 만들어진 것이 바로 여러 탐색 방법들입니다.

탐색 알고리즘의 종류는 여러 가지가 있습니다. 과학자들이 컴퓨터를 통해 많은 문제를 해결하기 위해 여러 탐색 방법을 만들어냈습니다. 지난 챕터에서 우리는 블라인드 탐색과 휴리스틱 탐색, 특히 언덕 오르기 탐색 방법도 알아보았습니다. 오늘 알아볼 것은 그 중에서 가장 휴리스틱적인 방법인 A* 알고리즘(에이스타 알고리즘)입니다.
그전에 잠깐, 휴리스틱이란 무엇인지 복습해볼까요? 휴리스틱이란 제한된 정보 내에서 직관적으로 판단하는 방법을 이야기합니다. 매우 익숙한 내용이죠. 왜냐하면 모든 인간은 이런 휴리스틱을 이용하기 때문입니다. 인간은 다양한 의사결정 상황에서 인지적으로 자신이 알고 있는 범위 내에서 판단하기 마련이죠.
휴리스틱이란?
휴리스틱(heuristics)은 한정된 시간 안에서 정확한 의사결정이 필요한 상황에서 빠르게 적용할 수 있는 방법입니다. ‘제한된 합리성’이라는 말로도 부르는데 다양한 의사결정 상황에서 인지적 한계 안에서 다룰 수 있는 범위로 축소시키고, 간단해진 과업의 수행에 한해 느슨하게 접근하는 것을 뜻합니다.
휴리스틱의 어원은 라틴어의 ‘heuristicus’ 와 그리스어 ‘heuriskein’ 에서부터 시작되었으며, “찾아내다(find out)” 그리고 발견하다(discover)”라는 의미를 뜻합니다.
시행과 착오를 거쳐 점점 나아가는 것도 휴리스틱이라 할 수 있으며 사실상 인간의 모든 활동은 휴리스틱에 의존합니다.

너무 쉬운 문제죠? 답을 굳이 표시하지 않더라도 100이면 100 같은 모양으로 선을 이었을 것입니다. 그것도 5초도 안되어서 말이죠. 근데 컴퓨터는 아마 이 문제를 푸는데 1분은 족히 넘게 걸릴겁니다. 왜냐하면 컴퓨터는 자신의 정답이 맞는지에 대한 확신이 없습니다. 따라서 인간은 한번 보고 직관적으로 답을 알아내기도 하지만, 컴퓨터는 가능한 모든 경우를 다 점검하려고 합니다.
수학에서는 이를 점이 7개므로 7!(7x6x5x4x3x2x1)의 문제로 볼 것입니다. 컴퓨터 역시 이 방법으로 계산하려면 인간보다 훨씬 더 많은 시간이 걸리게 됩니다. 7!를 계산하면 5,040입니다. 약 오천가지의 경우의 수를 구하고, 각각의 길을 비교해야 하기 때문입니다.
컴퓨터는 단순한 계산은 빨리하지만, 우리처럼 선택하는 문제는 상당히 오래 걸리게 됩니다. 따라서 이런 간단한 문제는 인간이 더 빠를 수 있는거죠. 인간에게 미로는 종이 위의 미로를 푸는 것 같지만, 컴퓨터에게 미로는 자신이 직접 들어가 있는 것과 같습니다. 더 나가기 어려운 쪽은 당연히 미로 안에 들어가 있는 쪽이겠죠.

그렇지만, 어려운 미로를 가져다 주면 상황은 달라집니다. 인간은 쉽게 포기하고 인지적 한계와 계산적 한계에 다다르지만 컴퓨터는 전기가 공급되는 한 한계란 걸 모르죠. 게다가 인간보다 계산 능력도 훨씬 좋습니다. 그래서 좋은 탐색 방법을 컴퓨터에게 가르쳐주고 컴퓨터에게 일을 시키는 겁니다.
오늘 배울 A* 알고리즘은 컴퓨터가 행하는 좋은 탐색 방법 중의 하나입니다.
다시 네비게이션으로 돌아와 볼까요? 인간도 결국에는 가장 좋은 길을 찾을 수 있습니다. 하지만 그날따라 막히는 도로는 어떻게 알 수 있을까요? 지금 당장 가야하는데 언제 길을 계산하고 갈까요? 그렇습니다. 그렇기 때문에 우리는 네비게이션이라는 훌륭한 도구를 사용합니다. 탐색 알고리즘을 활용하는 네비게이션을요.

정확히 말하면, 오늘 배울 A* 알고리즘은 현세대의 네비게이션에 사용되는 알고리즘은 아닙니다. 1968년에 발표된 오래된 알고리즘이죠. 하지만 가장 직관적인 알고리즘이면서 효율성도 좋아, 아직까지도 이 변형 알고리즘이 사용되는 경우가 많습니다. 또한 탐색 알고리즘의 가장 기본이기도 하죠. 한번 어떻게 동작하는지 알아보도록 합시다.
2. A* 알고리즘
이제 A* 알고리즘(에이스타 알고리즘)을 하나씩 알아보도록 합시다. 왜 이름은 A*라고 붙었을까요?
처음 개발한 피터 하트, 닐스 닐슨, 버트람 라팰이 이 알고리즘을 ‘알고리즘 A(Algorithm A)’라고 불렀기 때문입니다. 적절한 휴리스틱과 함께 사용하면 최적화된 알고리즘이 될 수 있습니다.
A* 알고리즘은 초기 상태에서 목표 상태까지 가는 최단 거리(혹은 비용)를 찾고자 하는 알고리즘입니다. 시작점부터 주변을 탐색하며 길을 찾아 나갑니다. 이 때, 다음에 나아갈 방향을 휴리스틱으로 평가하여 수치화 합니다. 예를 들어 목표 상태까지 가는 남은 거리를 휴리스틱으로 생각할 수 있습니다.
즉 A* 알고리즘은 “현재까지 지나온 거리 + 목표 상태까지 남은 거리” 가 최소인 길을 찾고자 합니다.
아래의 목표를 A*로 풀어보도록 하겠습니다.
목표 : A에서 Z까지 이동
조건 :
1. 장애물을 지날 수 없다.
2. 한 칸 옆으로 가는 데에는 거리를 10으로, 대각선으로 한번 이동하는 것은 14라고 한다.
3. 한번에 한칸만 이동할 수 있다.
이제 길을 찾아볼 단계입니다. A*에서 컴퓨터는 먼저 바로 다음에 갈 수 있는 칸들을 정합니다. 이 칸들의 집합을 오픈리스트(openlist)라고 합니다. A에서는 A를 둘러싼 8칸이 오픈리스트입니다.
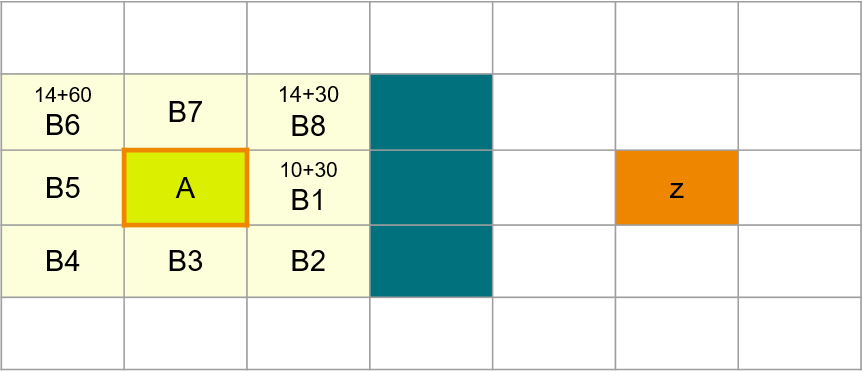
그럼 컴퓨터는 먼저 갈 수 있는 오픈리스트에서 값을 평가합니다. 평가는 간단합니다. 다음칸까지의 거리와 다음칸에서 목표지점까지의 거리입니다. 그럼 B1에서는 평가값이 무엇이 될까요?
A에서 B1까지 거리 10, 그리고 B1부터 Z까지의 거리 30으로 총 합이 30이 되겠죠.
그럼 딱 봐도 멀어보이는 B6로 간다고 해 봅시다.
그럼 B6까지의 거리 14, 그리고 B6부터 Z까지의 거리 60(오오오오오아래 화살표) 로 74가 됩니다.
그럼 30과 74가 있으면 당연히 덜 수고로운 30을 택할 것입니다. 자, 그럼 B1으로 이동합니다.
아 한가지 더, 자기가 처음 출발했던 A는 다시 가지 않을테니 Closed list에 넣어 가지 않을 칸으로 정해둡니다.
자 그럼 이제 B1에서 어디로 가야할까요, 막상 평가값이 40인 곳으로 오니 장애물이 있어 위와 아래밖에 갈 곳이 없습니다. 갈 곳이 B2, B3, B7, B8 밖에 없습니다. 물론 컴퓨터는 4개 다 계산해보겠지만 B2와 B8 중에 가겠죠.

어느쪽으로 가든 상관없으니 한군데를 선택할 것입니다. 아래쪽으로 간다고 해 봅시다. 그럼 A-B1-B2까지 총 거리는 10+10으로 20입니다. 앗, 그러면 A에서 바로 B2로 가는게 낫지 않았을까요? 아까야 장애물이 오픈리스트에 없었으니 몰랐지만, 지금은 알게되었으니 상황이 다르죠. 그럼 길을 바꿉니다. 장애물을 알게 된 이상 20보다 14가 더 나은 상황이 된거죠. 길을 갱신하도록 합시다.
이제 그럼 B2로 오게 되었습니다. B1은 방금 폐기되었으니 Closed List에 넣어두죠. 현재까지 온 거리는 14이입니다. 이제 갈 수 있는 B2주변 네 곳을 C로 확인해보겠습니다.
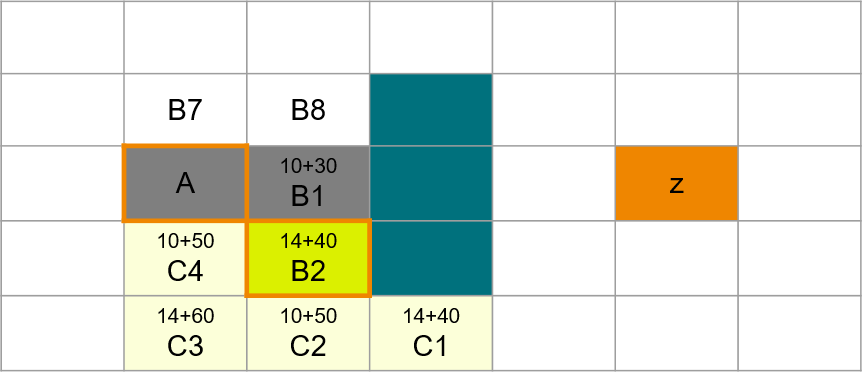
자 그럼 이번에는 지금까지 14에 더해 C1으로 가면 추가로 14를 더해 24에 앞으로 갈 거리 40으로 평가값이 64가 됩니다. C2로 가면 14+10+50= 74, C3는 14+14+60으로 무려 84네요. 당연히 C1으로 가게 됩니다. 장애물이 있어도 대각선으로는 갈 수 있다는 가정입니다.

그럼 이제 이 내용의 반복입니다. 같은 방식으로 지금까지 온 길 + 앞으로 갈 길을 평가해서 값이 가장 낮은 방향으로 이동할 것입니다. 이것의 반복으로 가게 되는 겁니다. 아주 휴리스틱적인 방법입니다.

왜냐하면 내가 지금 볼 수 있는 것은 내 주변에 붙어있는 칸이지만, 최종 목표점인 z를 향해서 가고자 자기가 가진 최소한의 정보들로 앞으로 계속 향해 가기 때문입니다.
이 방법도 여러가지 변형을 통해 더 나은 알고리즘을 만들어갈 수 있습니다. 지금처럼 자신의 주변 8칸을 전부 탐색하는 것을 맨해튼 거리 방법이라고 합니다. 미국의 맨해튼처럼 블록블록 건물들이 들어서 있는 모습을 말하는거죠. 이 방법 외에도 유클리디안 거리 방법, 체비쉐브 방법들이 있습니다. 평가값을 정하는 방법들이 조금씩 다르지만, 평가값을 통해 앞으로 나아가는 방법은 모두 똑같습니다.
3. A* 알고리즘 시뮬레이션
A* 알고리즘을 스크래치 프로그램을 통해 체험하여 봅시다.
[S]를 누르면 마우스의 현재 위치를 출발지로 설정합니다.
[스페이스바]를 누르면 현재 마우스 위치를 목적지로 설정합니다.
[R]을 눌러 스크린을 지우고 다시 시작할 수 있습니다.
빈 공간을 누르면 벽을 세울 수 있고, 벽을 누르면 장애물을 없앨 수 있습니다.
현재 탐색중인 위치는 노란색 블럭으로, Open list에 추가한 위치는 초록색 블럭으로, Closed list에 추가한 위치는 빨간색 블록으로 나타냅니다. 탐색을 끝낸 후 컴퓨터가 찾은 파란색 길이 A*알고리즘으로 찾은 가장 짧은 길입니다.
퀴즈
A*알고리즘에서 Closed List에 추가한 위치는 다시는 재방문하지 않는다.
Closed List에 추가한 것은 탐색을 끝냈으므로 다시 방문할 필요가 없다.
A* 알고리즘은 대표적인 휴리스틱 알고리즘이다.
현재 상태에서 목표 상태까지의 예상 거리(혹은 비용)은 휴리스틱 함수로 계산한다. 이 함수의 구체적인 식은 컴퓨터 개발자가 정하는 것이다.
