2. 베이즈 정리
2. 베이즈 정리
오늘 일기예보를 확인해보았습니다. 비가 올 확률이 70%입니다. 아침에 허겁지겁 나오느라 우산을 가지고 오지 않았습니다. 그래서 우산을 사려고 하는데 비가 올 것도 같고, 오지 않을 것 같기도 하여 우산을 사야 할지 말아야 할지 고민입니다.
아마 이렇게 고민해본 경험이 한번쯤은 있을 것입니다. 비가 올 확률이 높은데 우산을 가져오지 않아 우산을 구입해야 할지 고민한 경우가 있지요. 실제로 우산을 구입했을 때 비가 오지 않아 ‘아 괜히 샀네…’라며 후회한 적도 있을 겁니다. 그렇다면 우산을 구입했을 때 비가 올 확률을 예상할 수 있을까요?
베이즈 정리는 일어난 일을 토대로 일어나지 않은 일에 대한 확률을 구할 때 사용됩니다. 조건부 확률을 이용하여 사전 확률과 사후 확률 사이의 관계를 파악합니다. 위의 이야기를 예시를 토대로 다음과 같이 정리할 수 있습니다.
(사전 확률) 비가 올 확률
(조건부 확률) 비가 올 때 우산을 구입할 확률
(사후 확률) 우산을 구입했을 때 비가 올 확률
(사전 확률) P(A)
(조건부 확률) P(B|A)= P(A∩B) / P(A)
(사후 확률) P(A|B)= P(A∩B) / P(B) , P(B) > 0
사전 확률, 조건부 확률, 사후 확률은 위의 식처럼 표현할 수 있습니다. 여기에서 P(A)는 ‘A가 일어날 확률’ 이고, P(B|A)는 A일 때 B가 일어날 확률입니다. 사후 확률을 구하는 방법을 알아보겠습니다.
사전 확률, 조건부 확률, 사후 확률은 위의 식처럼 표현할 수 있습니다. 여기에서 P(A)는 ‘A가 일어날 확률’ 이고, P(B|A)는 A일 때 B가 일어날 확률입니다. 사후 확률을 구하는 방법을 알아보겠습니다.
‘P(A|B)= P(A∩B) / P(B)’ 을 구하기 위해서는 P(A∩B)와 P(B)를 구하는 방법을 알아보아야 합니다.
P(B|A)= P(A∩B) / P(A)의 식에서 P(A∩B)=P(A)P(B|A)를 도출할 수 있습니다. P(B)(우산을 살 확률)은 비가 올 때의 우산을 구입할 확률과 비가 오지 않을 때의 우산을 구입할 확률을 더해주면 됩니다.
즉, P(B)=P(A)P(B|A) + P(A’)P(B|A’)로 구할 수 있습니다. 정리하면 다음과 같습니다.
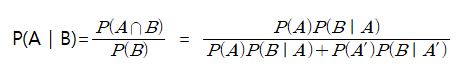
실제 이 과정을 토대로 ‘우산을 구입할 때 비가 올 확률’을 구해보겠습니다.

이와 같은 정보가 있습니다. 먼저 ‘P(B) – 우산을 구입할 확률’을 구해보겠습니다.
P(B) = P(A)P(B|A) + P(A’)P(B|A’)
= (0.7) × (0.3) + (0.3) × (0.1) = 0.21 + 0.03
= 0.24 (24%)
우산을 구입할 확률(P(B))은 24%가 나왔습니다. 이를 토대로 우산을 구입했을 때 비가 올 확률을 구해보겠습니다.
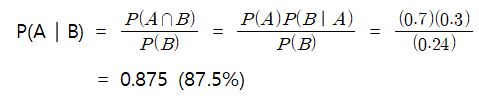
우산을 샀을 때 비가 올 확률은 87.5%가 됩니다.
2. 베이즈 정리
1. 베이즈 정리는 조건부 확률을 통해 사전 확률과 사후 확률의 관계를 파악하는 이론입니다.
2. 다음 설명이 맞으면 O, 틀리면 X를 선택하세요.

3. 알맞은 값을 골라 보세요.

- P(B) = P(A)P(B|A) + P(A’)P(B|A’) = 0.30.2 + 0.70.1 = 0.06 + 0.07 = 0.13 (13%) - P(A|B) = 0.3×0.2/0.13 = 0.4615 (46.2%)